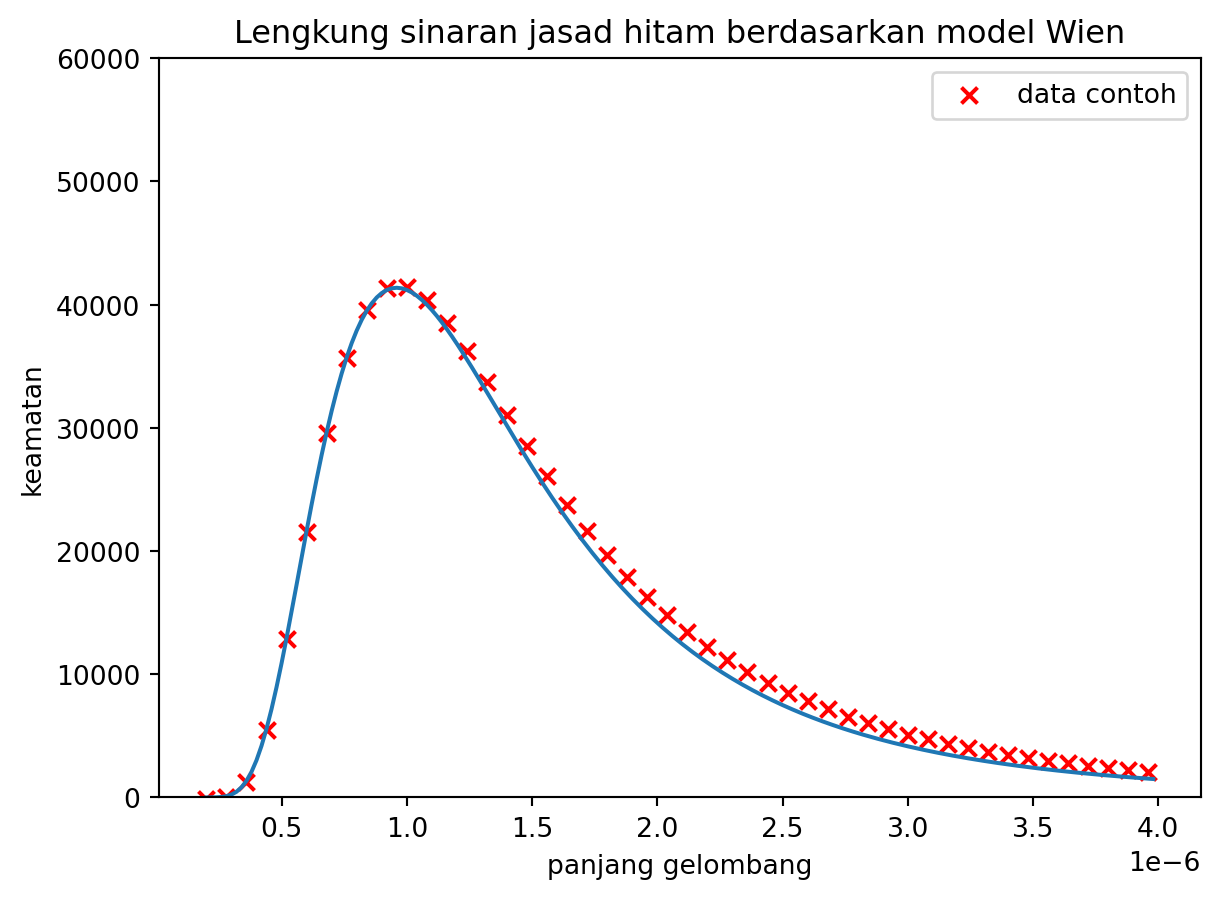
3 Hukum Taburan Wien
3.1 Kaitannya Dengan Hukum Planck
Proof. Hukum taburan Wien boleh menerangkan lengkung jasad hitam dengan baik hanya jika panjang gelombangnya pendek. Ia gagal untuk panjang gelombang panjang. Maka, kita boleh peroleh hukum taburan Wien jika diletakkan syarat panjang gelombang mesti pendek.
Hukum taburan Wien boleh diperolehi jika panjang gelombang, \(\lambda\), dihadkan ke arah sifar dalam hukum Planck, \[ U_{\text{Wien}}=\lim_{\lambda\to 0}\frac{8\pi hc}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k_BT}}-1}. \tag{3.1}\]
Lalu, kita perhatikan apa yang terjadi pada sebutan eksponennya. Jika \(\lambda\) menghampiri sifar, maknanya \(\frac{hc}{\lambda k_BT}\) akan menjadi tersangatlah besar. Maka nilai \(1\) itu boleh diabaikan seperti dalam petua 3.1.
Petua 3.1 (Penghampiran Eksponen ke Arah \(\infty\)) \[ \lim_{x\to\infty}e^x - 1 \approx e^x. \]
Oleh itu, pers. 3.1 menjadi, \[ U_{\text{Wien}}=\frac{8\pi hce^{-\frac{hc}{\lambda k_BT}}}{\lambda^5}, \] yang sepadan dengan hukum taburan Wien. Jika dibandingkan dengan pers. 3.1, kita akan dapat kira nilai pemalar \(a\) dan \(b\), \[ a = 8\pi hc,\;b = \frac{hc}{k_B}. \]