Lampiran A — Penyelesaian Berkomputer Untuk Sesaran Wien

Pers. 5.7 yang muncul dalam bahagian 5.1 berbentuk begini \[ X\frac{e^X}{e^X-1} = 5. \tag{A.1}\]

Agak sukar untuk menyelesaikan persamaan ini pakai tangan jadi kita rujuk kaedah berangka.

Note

Secara ringkasnya, kaedah berangka cuba mendapat jawapan penghampiran melalui pemanipulasian angka. Bandingkan dengan kaedah beraljabar yang mendapat jawapan tepat melalui mantik terhadap simbol. Contoh kaedah berangka ialah pencarian titik silang antara graf dengan garis \(y=0\) melalui cuba jaya berulang kali.

Bagi mendapatkan nilai \(X\) dalam pers. A.1, kita harus akui ia sama dengan \[ X\frac{e^X}{e^X-1} - 5 = 0 \] lalu kita gantikan 0 menjadi pembolehubah \(y\), \[ X\frac{e^X}{e^X-1} - 5 = y. \tag{A.2}\] Persamaan ini mewakili graf \(x\) melawan \(y\). Nilai \(X\) yang kita mahukan ialah apabila \(y=0\). Permasalahan ini telah bertukar menjadi permasalahan pencarian titik silang graf dengan garis \(y=0\).

A.1 Kaedah Pembahagi Dua

Kaedah paling mudah nak faham dan buat untuk mencari titik silang graf dengan garis \(y=0\) ialah kaedah pembahagi dua. Langkah-langkahnya ialah seperti berikut:

  1. Pilih dua titik, kiri dan kanan. Jauh-jauh pun tidak mengapa asalkan titik persilangan itu berada di antara dua titik ini.
  2. Dapatkan titik tengah lalu kita peroleh dua julat: julat [kiri, tengah] dan julat [tengah, kanan].
  3. Semak samada persilangan berlaku dalam julat pertama atau tidak. Persilangan ini boleh disemak dengan melihat sama ada dua nilai tersebut berbeza tanda positif atau negatifnya.
    • Jika ya, maka balik ke langkah (1) dengan nilai baharu kiri=kiri dan kanan=tengah.
    • Jika tidak, kita andaikan persilangan berlaku dalam julat kedua. Balik ke langkah (1) dengan nilai baharu kiri=tengah dan kanan=kanan.
  4. Ulang langkah (1) sampai (3) sehingga jarak antara kiri dan kanan lebih kecil dari ketepatan yang diinginkan. Ambil nilai tengah sebagai jawapan.

A.1.1 Pelaksanaan

🐍 Python serta Sandaran-Sandarannya

Kod yang dipaparkan dalam dokumen ini diuji menggunakan Python versi 3.10.12 bersama sandaran-sandaran berikut:

  1. numpy=1.25.0
  2. matplotlib=3.7.1
```{python}
def persilangan_pembahagi_dua(
        fungsi, # fungsi yang kita nak tahu puncanya (titik persilangan)
        kiri: float, 
        kanan: float, 
        ketepatan: float = 1.0e-6
    ) -> float:

    # [1] Pilih dua titik, `kiri` dan `kanan`.
    jarak = abs(kanan-kiri)
    
    had: int = 100 # Untuk letak had berapa kali boleh ulang
    ulangan: int = 1 # Untuk kira berapa kali dah ulang

    while jarak > ketepatan:
        # [2] Dapatkan titik `tengah`
        tengah = (kiri+kanan)/2.
        
        # [3] Semak sama ada ada persilangan berlaku
        #     di julat pertama [`kiri`,`tengah`]
        if (fungsi(kiri)*fungsi(tengah)) < 0:
            # Jika ya:
            # Balik ke langkah (1) dengan nilai baru kiri=kiri dan kanan=tengah
            # Ulangan [1] Pilih dua titik, `kiri` dan `kanan`.
            kiri = kiri
            kanan = tengah
        else:
            # Jika tidak:
            # Balik ke langkah (1) dengan nilai baru kiri=tengah dan kanan=kanan
            # Ulangan [1] Pilih dua titik, `kiri` dan `kanan`.
            kiri = tengah
            kanan = kanan
        # [4] Ulang langkah [1] - [3] sampai `jarak <= ketepatan`
        jarak = abs(kanan-kiri)

        # Kalau dah lebih had, kita keluar. 
        # Kita tak nak benda ni ulang sampai kiamat tak berhenti.
        ulangan += 1
        if ulangan == had: 
            raise ValueError(
                f'Sudah {had} kali diulang tetapi masih tak jumpa jawapan.'
                )
    
    return tengah
```

A.1.2 Kelebihan dan Kekurangan

  • Kelebihan kaedah ini ialah ia sangat mudah dan sangat cekap. Jika titik persilangan berada di antara dua titik asal, maka kita akan jumpa titik persilangan itu.
  • Kekurangan kaedah ini ada dua:
    1. Kaedah ini tidak begitu pantas. Sekiranya titik asal kiri dan kanan berpisah jauh sangat, maka pencarian titik persilangan akan ambil masa yang lama kerana jaraknya hanya dibahagi dua setiap kali.
    2. Kaedah ini mengandaikan titik persilangan berada di antara titik kiri dan kanan yang awal. Sekiranya tidak, maka kaedah ini tidak akan membuahkan apa-apa hasil.

A.2 Penyelesaian

Sebelum kita mulakan penyelesaian, kita perlu tahu dahulu adakah fungsi yang kita ada ini bersilang dengan garis \(y=0\) tidak? Kita cuba lukis graf untuk tengok wujud ke tak persilangan tersebut. Oleh itu, kita takrifkan dulu fungsi untuk pers. A.2.

```{python}
import numpy as np

def formula(x: float) -> float:
    return x*np.exp(x)/(np.exp(x) - 1) -5
```

Kemudian, bolehlah kita lukis grafnya.

```{python}
import matplotlib.pyplot as plt

x = np.linspace(0.1, 10)
y = formula(x)

plt.plot(x, y)
plt.axhline(y=0, linewidth=0.8, color='black')
plt.show()
```

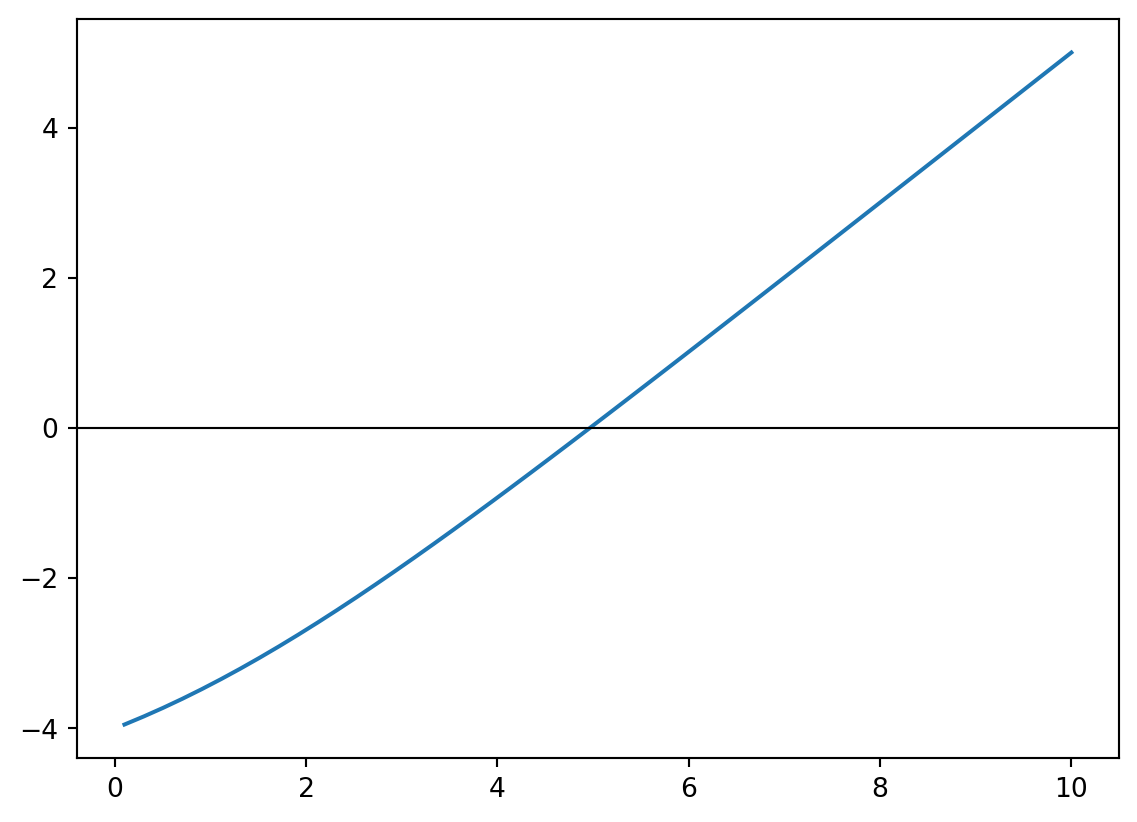
Nampaknya, titik persilangan tersebut berada di antara \(x=4\) dan \(x=6\). Kedua-dua nilai ini boleh jadi nilai kiri dan kanan asal untuk kaedah pembahagi dua.

Apabila sudah diketahui wujud titik persilangan, maka bolehlah kita gerakkan algoritma pencarian titik silang melalui pembahagian dua.

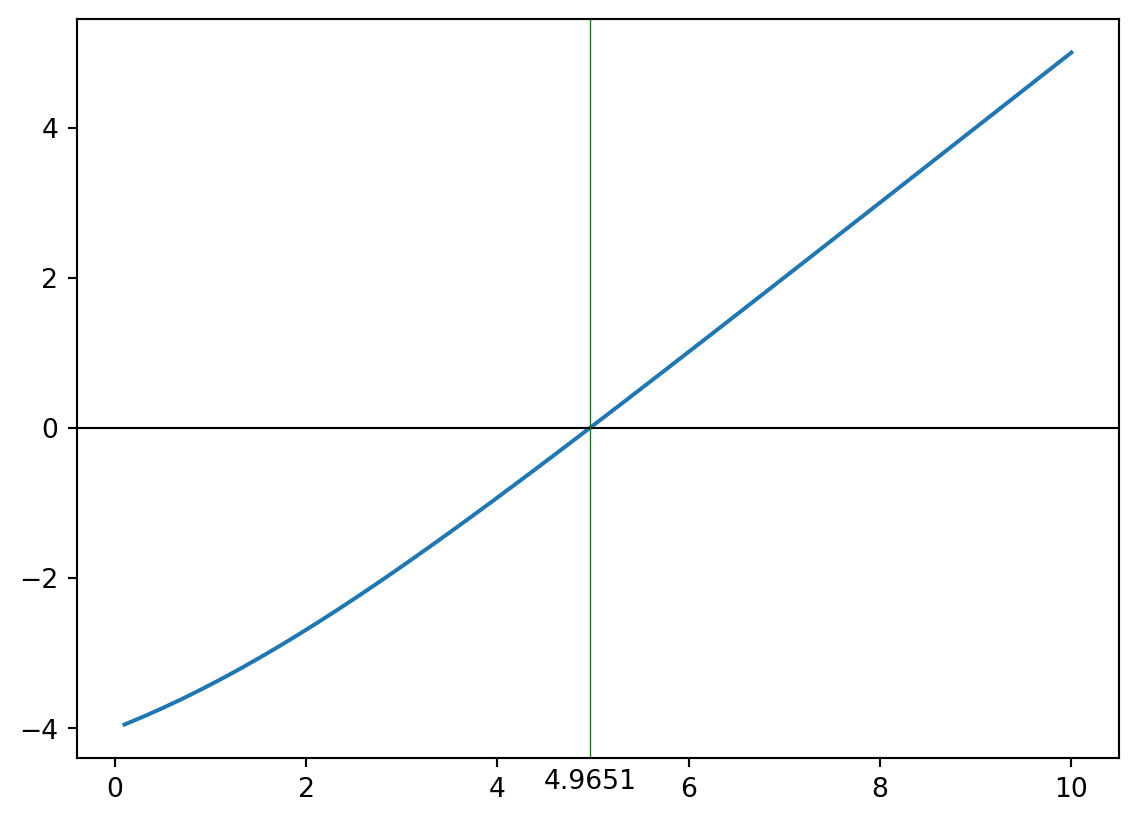
```{python}
jawapan = persilangan_pembahagi_dua(formula, kiri=4, kanan=6)
```
Nilai x ialah 4.965113639831543 apabila y=0

Kita boleh semak jawapan ini dengan graf.