4 Hukum Rayleigh–Jeans
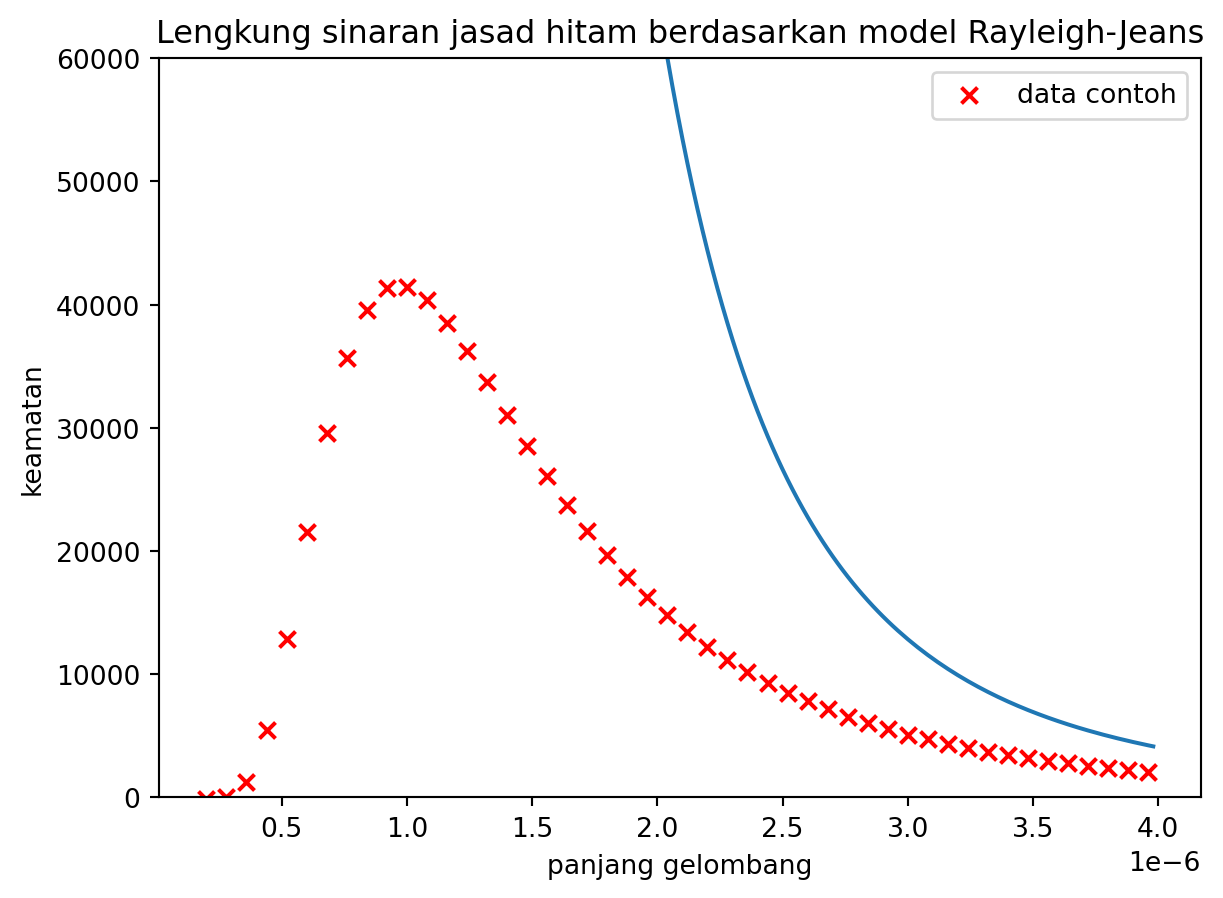
Hasil daripada persamaan Rayleigh–Jeans ialah suatu graf yang menghampiri sifar untuk panjang gelombang yang panjang, tetapi akan menghampiri infiniti untuk panjang gelombang pendek. Hakikat ini nyata bagi yang celik Matematik kerana persamaan Rayleigh–Jeans ialah suatu fungsi salingan, \(\frac{1}{x}\), berkuasa 4.
Maknanya, menurut persamaan ini, bintang akan memancarkan cahaya berpanjang gelombang pendek dengan tenaga yang tidak terhingga! Perkara ini adalah mustahil kerana ia melanggar hukum keabadian tenaga seolah-olah jisim yang terbatas boleh menghasilkan tenaga yang tidak terbatas.
Kejadian ini lazimnya diberi nama “Malapetaka Ultralembayung” kerana sifat gelombang ultralembayung yang pendek panjang gelombangnya. Walaupun tiada malapetaka sebenar yang meragut mana-mana nyawa, nama itu sedap disebut dan selari dengan naluri manusia yang sukakan cerita menarik maka ia melekat dalam lidah para fizikawan.
4.1 Kaitannya dengan Hukum Planck
Proof. Hukum Rayleigh–Jeans boleh menerangkan lengkung jasad hitam pada panjang gelombang panjang. Oleh itu, kita boleh peroleh hukum Rayleigh–Jeans jika diletakkan syarat panjang gelombang mesti panjang.
Hukum Rayleigh–Jeans boleh diperoleh jika dihadkan panjang gelombang, \(\lambda\) menghampiri infiniti dalam hukum Planck, \[ U_{\text{RJ}} = \lim_{\lambda\to\infty}\frac{8\pi hc}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k_BT}}-1}, \tag{4.1}\]
Kemudian, apabila melihat pada eksponennya, kita dapati \(\frac{hc}{\lambda k_BT}\) menghampiri sifar kerana \(\lambda\) menghampiri infiniti.
Petua 4.1 (Penghampiran Eksponen ke Arah 0) \[ \lim_{x\to 0} e^x \approx x + 1. \]
Bila petua 4.1 digunakan terhadap pers. 4.1, kita dapati bahawa hanya sebutan \(\frac{hc}{\lambda k_BT}\) sahaja yang tinggal, \[ \lim_{\lambda\to\infty} e^{\frac{hc}{\lambda k_BT}}-1 \approx \frac{hc}{\lambda k_BT}+1 -1=\frac{hc}{\lambda k_BT}. \tag{4.2}\]
Kita peroleh persamaan ini, \[ U_{\text{RJ}} = \frac{8\pi hc}{\lambda^5}\frac{1}{\frac{hc}{\lambda k_BT}}, \] yang setara dengan, \[ U_{\text{RJ}} = \frac{8\pi}{\lambda^4}{k_BT}, \] iaitu persamaan Rayleigh–Jeans yang ingin kita perolehi.