Rakyat Malaysia secara umumnya menggunakan kertas bersaiz A4 untuk menulis, melukis, membalas surat cinta dan pelbagai kegunaan umum yang lain. Malah, ianya digunakan di pelbagai negara secara meluas kecuali negara-negara yang menggunakan sistem kertas Amerika (seperti Amerika Syarikat, Kanada dan Mexico). Tahu tak kertas A4 ini sangat bijak sampai Pelawak Matematik Matt Parker sempat mempermainkan sistem kertas Amerika?
Matematik Di Sebalik Kertas A4.
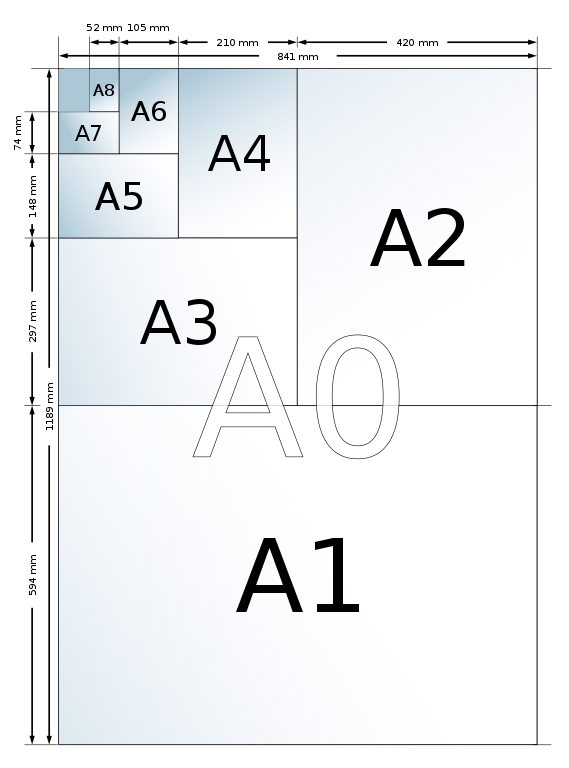
Ilustrasi pembahagian sekata kertas siri A. Perhatikan bagaimana nisbah sisi:panjang dikekalkan (Imej milik Sven, Lesen CC-BY-SA 3.0)
Umum mengetahui kalau kita bahagikan kertas A3 kepada dua akan menjadi A4 dan A4 kalau dibahagikan lagi akan menjadi A5 maka begitu jugalah seterusnya. Maknanya, nisbah sisi kepada panjang (sisi:panjang) kertas akan kekal sama walau dibahagikan. Nisbah ini dikemukakan oleh ahli fizik Georg Christoph Lichtenberg dalam suratnya kepada Johann Beckmann dengan alasan mana-mana bahagian dalam kertas A4, misalnya, tidak akan hilang jika dipindahkan kepada kertas yang lebih kecil dengan pengecilan yang sekata. Piawaian saiz pula ditetapkan oleh Perancis pada tahun 1798 (ISO 216).
Kertas siri A (A0-A10) menggunakan nisbah sisi:panjang yang sama iaitu \(1:\sqrt{2}\). Malah, itu sahajalah satu-satu nisbah yang membolehkan kertas A4 mempunyai sifat yang diterangkan di atas. Berikut ialah pembuktian matematik:

Dengan nisbah ini sahajalah kertas A4 mampu mempunyai sifat istimewa ini.
Berapa pula nilai \(\sqrt{2}\) ?!
“Hah?! Wujud pula 2 punca kuasa dua? Setahu saya hanya 1, 4, 8, 16, 25 dan seterusnya (12, 22, 32, 42, 52 … n2) boleh ada punca kuasa dua!” Seorang pembaca setia dengan setianya ingin membantah.
Sabar! Sememangnya nombor-nombor itu sahaja yang ada punca kuasa dua bernombor bulat atau kita panggil ‘kuasa dua sempurna’. Maknanya kita akan dapat nombor yang boleh dinisbahkan apabila kita mencari punca kuasanya. Bagaimana pula dengan 2 punca kuasa dua?
Nombor \(\sqrt{2}\) adalah nombor tiada nisbah seperti \(\pi\) (pi) dan \(e\) (nombor Euler). Seperti mana-mana nombor tiada nisbah, nombor perpuluhan \(\sqrt{2}\) tiada penghujung dan nombor ini tidak boleh ditulis dalam bentuk pecahan. Maka, untuk mendapatkan \(\sqrt{2}\) kita perlukan pentakrifan nilai menggunakan satu fungsi. Yang menariknya, nombor tiada nisbah berpunca kuasa dua boleh dapatkan takrifan menggunakan fungsi trigonometri (dan pembuktian geometri).
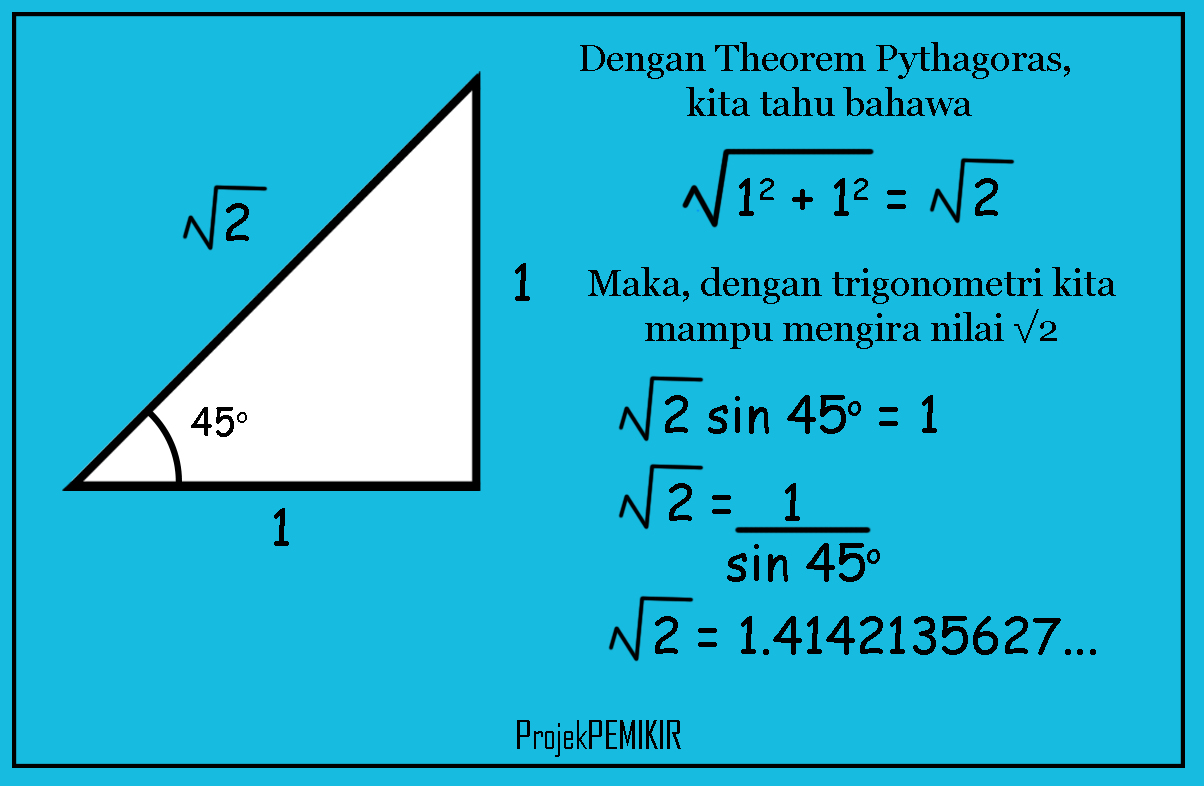
Taktik yang sama boleh digunakan untuk mencari \(\sqrt{3}\), \(\sqrt{4}\), \(\sqrt{5}\), \(\sqrt{6}\), dan seterusnya.
Maka, nilai \(\sqrt{2}\) ialah \(1.41421\dots\)
Kesimpulan
Sangat menarik bagaimana teknologi seringkas kertas juga memerlukan matematik untuk memberikan sifat yang kalian tahu secara umum. Menarik lagi bagaimana sifat yang nampaknya ringkas itu (bahagi dua untuk jadi kertas lain tapi sama nisbah) menggunakan nombor yang nampak remeh. Oh, betapa indahnya dunia Matematik!